Simulation numérique pour le délaminage des
composites:
Le code d'éléments finis SAMCEF propose des solutions pour modéliser et
analyser le délaminage dans les structures composites. Deux approches basées
sur la mécanique de la rupture et sur la théorie des dommages sont
présentées ici, avec une illustration de la propagation de fissures
interlaminaires sous charge statique sur une application industrielle.
(Traduction de l'article publié en Juin 2008 -
JEC Magazine N°41)
Grâce à leur rapport rigidité / poids élevé et à leurs propriétés
anisotropes, les matériaux composites sont largement utilisés dans
différents secteurs tels que l'énergie, la marine, l'automobile, le
bâtiment et la construction, et, bien sûr, l'aéronautique. L'un des modes
de rupture prédominants dans les composites multicouches est la
délamination, qui résulte d'une séparation des couches adjacentes à des
emplacements sensibles aux effets transversaux. Si le nombre de fissures
initiées est élevé, les propriétés mécaniques globales des structures
laminées réelles peuvent être diminuées. Ceci est particulièrement vrai
pour les structures aérospatiales constituées de panneaux minces avec des
cadres et des raidisseurs co-durcis ou collés. Pour fournir des composants
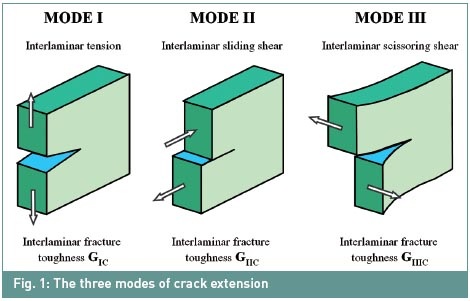
sûrs, il est donc obligatoire de tenir compte de ces défauts lors de la
phase de conception (figure 1) et de vérifier l'intégrité structurale
pendant leur propagation.
Cependant, évaluer la tolérance aux dommages
des structures composites est clairement un défi. D'un autre côté,
l'utilisation de tests numériques réduit le nombre de prototypes physiques
requis et le délai d'exécution.
Le code d'éléments finis SAMCEF propose des
solutions pour simuler et analyser la délamination des composites. Ici,
seul le cas du chargement statique est évoqué. SAMCEF Asef et SAMCEF
Mecano sont utilisés, pour des analyses linéaires et non linéaires,
respectivement.
La méthode de propagation de fissure
virtuelle
La première approche disponible dans
SAMCEF pour évaluer les risques de
délaminage consiste à utiliser la mécanique de la rupture dans une analyse
statique (éventuellement linéaire). Les taux de libération d'énergie de
contrainte par mode, GI, GII et GIII, sont calculés avec la méthode
Virtual Crack Extension (VCE) comme expliqué dans la figure 2.
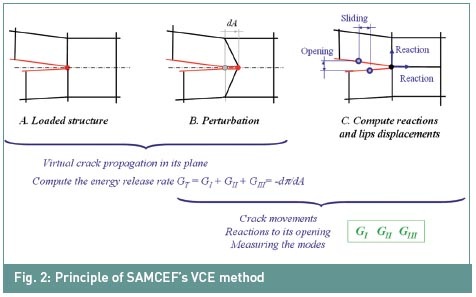
La variation de l'énergie
potentielle totale par rapport à un incrément de surface de fissure
virtuel donné dA est d'abord calculée pour le champ de déplacement actuel
(d'équilibre) via une analyse de sensibilité semi-analytique. Ceci fournit
le taux de libération d'énergie totale GT, qui est une mesure de la façon
dont la rigidité diminue quand une fissure se propage. Ensuite, la
contribution aux trois modes individuels est mesurée, en fonction des
mouvements relatifs des lèvres pendant le chargement et des réactions
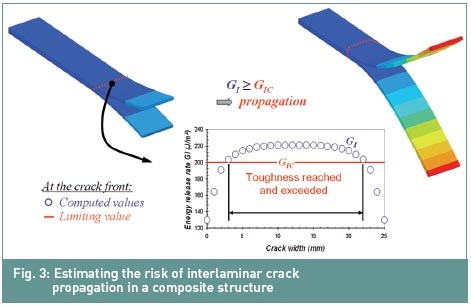
contre la propagation des fissures. En comparant ces valeurs à la ténacité
à la rupture interlaminaire, GIC, GIIC et GIIIC, sur la base de certains
critères, les fissures critiques peuvent être identifiées et la charge de
propagation associée peut être estimée (figure 3).
L'approche des éléments
cohésifs
Dans la seconde approche, la
mécanique de la rupture est utilisée en
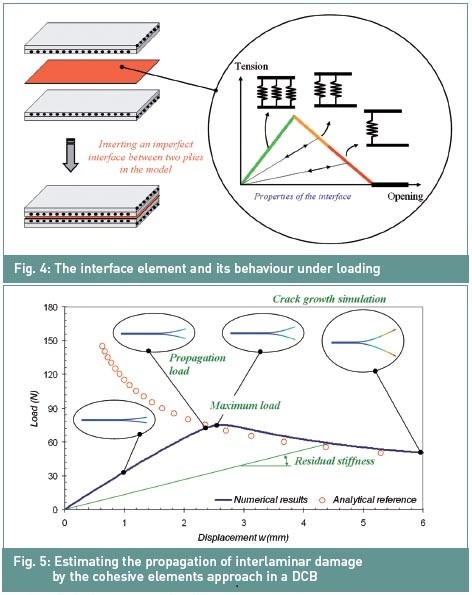
conjonction avec un modèle d'endommagement interlaminaire. Afin de
représenter cet endommagement interlaminaire éventuel, une couche mince
est insérée entre deux plis du stratifié, comme représenté sur la figure
4. Une spécifité non-linéaire
Une loi de ramollissement est assignée au
matériau dans cette couche mince, et sa rigidité et sa résistance peuvent
diminuer jusqu'à zéro pendant la période de chargement, simulant une
décohésion entre les couches. Une loi matérielle bi-triangulaire est
présentée dans la figure 4. Des lois polynomiales et exponentielles sont
également disponibles dans SAMCEF. Au détriment d'une analyse non
linéaire, cette stratégie permet d'estimer non seulement la charge de
propagation mais aussi la charge maximale et la raideur résiduelle au
cours du processus de fracture (figure 5).
Etude de cas industriel
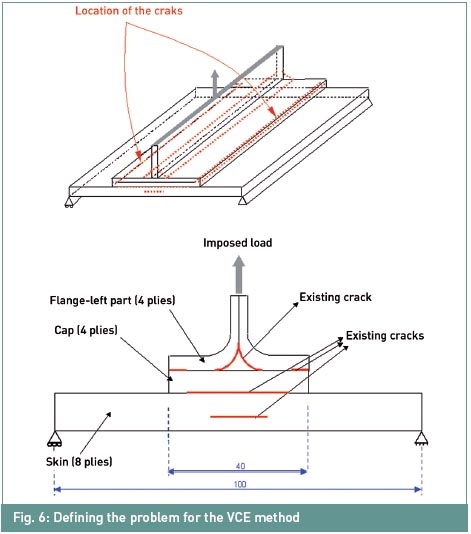
Une première structure composite raidie
multi-délaminée est considérée (figure 6). Il comprend neuf fronts de
fissures définis sur toute la longueur. Une force est imposée sur le
sommet du raidisseur, et les taux de libération d'énergie par mode, GI,
GII et GIII, sont calculés et inclus dans un critère de défaillance.
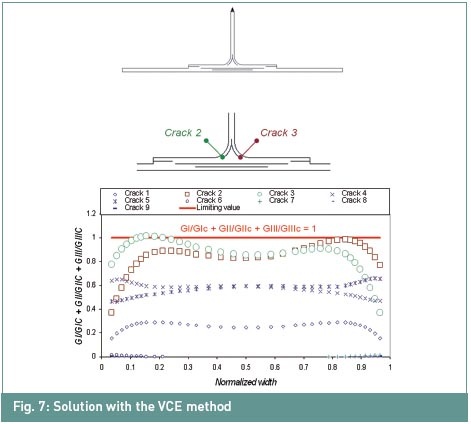
L'évolution de ce critère de rupture est
illustrée à la figure 7.
Lorsque sa valeur atteint 1, une propagation
de fissure se produit. Dans notre exemple, on peut observer que les
fissures 2 et 3 sont les plus critiques. Nous considérons maintenant un
deuxième panneau composite raidissé multi-délaminés qui comprend 55 fronts
de fissure initiaux entre chaque couche de peau et à l'emplacement des
noeuds, et deux grandes fissures entre le capuchon et les brides de
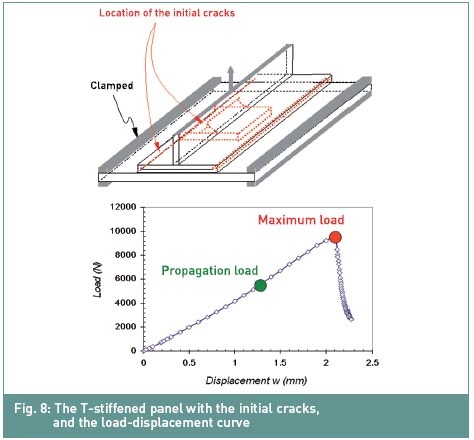
raidisseur (figure 8).
Ici, l'approche des éléments cohésifs est
utilisée pour analyser la propagation des dommages interlaminaires. Un
déplacement est imposé sur la partie supérieure du raidisseur en T. La
courbe charge-déplacement résultant de la simulation est fournie à la
figure 8, où la charge maximale admissible avant une perte significative
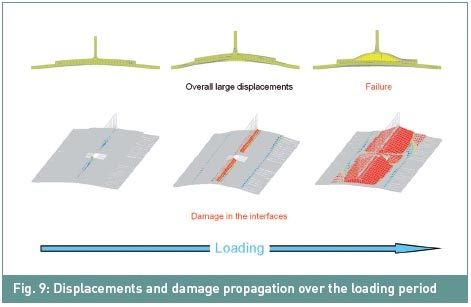
de la rigidité globale peut être estimée. Les déplacements structurels et
l'extension des dommages sur le chargement sont illustrés sur la figure 9.
Résumé:
La modélisation et la résolution des
problèmes de délamination dans les composites sont connues pour être
difficiles, et les capacités de test numérique offertes par SAMCEF sont
conformes à la réalité industrielle. Certains des besoins identifiés au
niveau industriel comprennent l'utilisation de modèles d'éléments finis de
grande taille pour représenter efficacement la réalité; prendre en compte
un grand nombre de fissures dans la structure afin de fournir une
conception sûre; modélisation des conditions de contact sur de grandes
surfaces; et obtenir des résultats précis. SAMCEF répond efficacement à
ces préoccupations industrielles avec des caractéristiques telles que la
définition des fissures et des zones de délamination; estimation rapide de
la charge de propagation via la méthode VCE; des capacités plus avancées
grâce à l'approche des éléments cohésifs pour la propagation des fissures
interlaminaires et l'estimation du comportement structural global au cours
du processus de fracture; une bibliothèque de lois matérielles
adoucissantes pour les comportements interlaminaires; stratégies efficaces
pour traiter les conditions de contact; résultats précis (comparés aux
solutions de référence); et une procédure de solution parallèle pour les
problèmes à grande échelle.